二极管等效电阻

一、二极管等效电阻

二极管等效电阻的重要性及其计算方法

在电子工程和模拟电路设计中，二极管等效电阻是一个重要的概念。它对于理解电路的工作原理，以及正确设计、分析和优化电路有着至关重要的作用。首先，让我们了解什么是二极管的等效电阻。

二极管的等效电阻是在电路中表示二极管的电阻值。它是由二极管的PN结构成，可以视为一个理想的电阻器。在实际应用中，二极管的性能会受到温度、制造工艺等因素的影响，因此等效电阻也会有所不同。然而，在大多数情况下，我们可以将二极管视为一个接近理想的电阻器。

如何计算二极管的等效电阻

二极管的等效电阻可以通过不同的方法进行计算。最常用的方法是使用半导体手册中提供的公式。该公式基于二极管的型号和参数，通常需要已知的电流和电压值。根据公式，可以计算出二极管的等效电阻值。

此外，还可以通过测量二极管的直流电阻值来估算其等效电阻。直流电阻通常比交流电阻高，因此在实际应用中，可以使用交流电源来测量二极管的等效电阻。

二极管等效电阻的应用

二极管等效电阻在模拟电路中起着至关重要的作用。它不仅可以用来分析和理解电路的工作原理，还可以用来优化电路性能。例如，通过控制二极管的等效电阻，可以调整电路的增益、带宽和延迟时间等参数。

此外，在模拟滤波器、功率MOSFET和IGBT驱动电路以及电池保护电路中，二极管等效电阻也起着非常重要的作用。

结论

总之，二极管等效电阻是电子工程和模拟电路设计中不可或缺的一部分。正确理解和应用二极管的等效电阻对于设计、分析和优化电路至关重要。通过使用半导体手册中的公式或测量直流电阻值来估算等效电阻，可以更好地理解其在实际应用中的意义。

二、二极管等效电阻 推导？

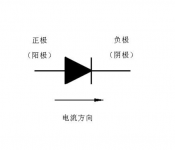
二极管电流方程id=Is(e^(Ud/Ut)-1)≈Ise^(Ud/Ut)由于[e^(nx)]'=e^(nx)/n ,所以 d（id）/d(Ud)=[Ise^(Ud/Ut)]/Ut≈id/Ut.

三、发光二极管 等效电阻？

发光二极管正向流过阻值为零，逆向流过阻值无穷大，所以不能用来当等效电阻

四、发光二极管的等效电阻？

发光二级管本来就属于电阻性元件，和普通电阻的不同在于它是非线性电阻，其阻值随工作电压、电流而变化，如果通过发光二极管的电流要很稳定（最好环境温度也是稳定的），那么它的电阻也会是一个较稳定的值，如果电流有明显变化，那么发光二极管的等效电阻也会发生明显改变。

五、电阻并联的等效电阻计算及应用

电阻并联相当于在电路中将多个电阻连接在一起，形成一个并联的电阻网络。并联电阻能够改变电路的整体电阻值，对电路的性能和功能有着重要影响。

电阻并联的原理

在电路中，当多个电阻与电源相连接，并且每个电阻之间是并联的，即它们的两端分别与相同两个节点相连时，就形成了电阻并联。

在电阻并联中，所有的电阻都连接在相同的两个节点上。这意味着它们之间的电压相同。根据欧姆定律，电阻值越大，通过电阻的电流越小。

因此，当电阻并联时，电路中的总电流将分流到并联的每个电阻上，并且每个电阻的电流值将与它的电阻值成反比。

由于电阻并联中的电流分流，不同电阻之间的电流是独立的，因此每个电阻之间都是独立的电路分支。这使得电阻并联的等效电阻计算相对简单，可以使用并联电阻的倒数之和来表示。

电阻并联的等效电阻计算

电阻并联的等效电阻（记作Req）可以通过以下公式进行计算：

1/Req = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn

其中，R1、R2、R3等表示各个并联的电阻值。

通过计算每个电阻的倒数之和，再将结果取倒数，即可得到电阻并联的等效电阻。

需要注意的是，在计算等效电阻时，电阻值必须使用相同的单位。

电阻并联的应用

电阻并联在电路中有着广泛的应用。以下是一些常见的应用场景：

• 调节电路的总电阻：通过将不同的电阻与电阻并联，可以改变电路的总电阻，从而调节电路的性能。
• 分压电路：在分压电路中，使用电阻并联来分配电压，使得电路中的不同部分能够获得所需的电压。
• 电阻网络：电阻并联可以用来构建复杂的电阻网络，用于各种电路的设计和分析。
• 电源隔离：通过将电阻并联到电源和负载之间，可以实现电源与负载的隔离，以保护电路和设备。

总之，电阻并联是电路中常用的连接方式，通过调整电阻的数量和数值，可以对电路的特性进行灵活的控制和调节。

感谢您阅读本文，希望可以帮助您更好地理解电阻并联的原理、计算方法和应用场景。

六、电阻等效单位？

导体的电阻通常用字母R表示，电阻的单位是欧姆（ohm），简称欧，符号是Ω（希腊字母，读作Omega)。1Ω=1V/A。比较大的单位有千欧（kΩ）、兆欧（MΩ）（兆=百万，即100万）。

电阻是一个物理量，在物理学中表示导体对电流阻碍作用的大小，它的英文名称为resistance，通常缩写为R，它是导体的一种基本性质，与导体的尺寸、材料、温度有关。导体的电阻越大，表示导体对电流的阻碍作用越大。不同的导体，电阻一般不同。电阻的基本单位是欧姆，用希腊字母“Ω”来表示。欧姆定律指出电压、电流和电阻三者之间的关系为I=U/R，亦即R =U/I。

他们的换算关系是:

1TΩ=1000GΩ；1GΩ=1000MΩ；1MΩ=1000KΩ；1KΩ=1000Ω（也就是一千进率）

七、串并联电阻的等效电阻计算方法

引言

在电路中，电阻是一种常见的元件，它用于控制电流的流动。当电路中存在多个电阻时，我们需要计算它们的等效电阻，以便更好地理解电路的特性。本文将介绍串联电阻和并联电阻的概念以及计算等效电阻的方法。

串联电阻

串联电阻是指将多个电阻依次连接在一起，电流依次通过每个电阻。在串联电路中，电流在电阻之间没有分支，其总电阻等于各个电阻之和。假设有两个电阻R1和R2串联连接在一起，它们的等效电阻R_eq可以通过以下公式计算：

R_eq = R1 + R2

并联电阻

并联电阻是指将多个电阻同时连接在一起，它们的两端相连。在并联电路中，电流会分流通过不同的电阻，各个电阻的电压相同。在计算等效电阻时，可以使用以下公式：

1 / R_eq = 1 / R1 + 1 / R2

应用实例

接下来通过一个实例来说明如何计算串并联电阻的等效电阻。假设有三个电阻，它们的阻值分别为12Ω，18Ω和24Ω。首先计算串联电阻的等效电阻：

R_eq = 12Ω + 18Ω + 24Ω = 54Ω

然后计算并联电阻的等效电阻：

1 / R_eq = 1 / 12Ω + 1 / 18Ω + 1 / 24Ω = 0.1389Ω

最后求得等效电阻：

R_eq = 1 / 0.1389Ω = 7.2Ω

总结

串并联电阻的等效电阻计算方法如上所述。在串联电路中，电阻之和等于等效电阻；在并联电路中，电阻的倒数之和的倒数等于等效电阻。通过计算等效电阻，我们可以更好地理解电路中电阻的特性，从而分析和设计电路。

感谢您的阅读

感谢您阅读本文，希望通过本文的介绍，您对串并联电阻的等效电阻计算方法有了更好的理解。无论是在学习电路知识还是在实际应用中，这些计算方法都将为您提供帮助。

八、等效电阻化简？

　几个连接起来的电阻所起的作用，可以用一个电阻来代替，这个电阻就是那些电阻的等效电阻。也就是说任何电回路中的电阻，不论有多少只，都可等效为一个电阻来代替。而不影响原回路两端的电压和回路中电流强度的变化。这个等效电阻，是由多个电阻经过等效串并联公式，计算出等效电阻的大小值。也可以说，将这一等效电阻代替原有的几个电阻后，对于整个电路的电压和电流量不会产生任何的影响，所以这个电阻就叫做回路中的等效电阻。

　　就是用一个电阻代替串联电路中几个电阻，比如一个串联电路中有2个电阻，可以用另一个电阻来代替它们。首先把这两个电阻串联起来，然后移动滑动变阻器，移动到适当的地方就可以，然后记录下这时的电压与电流，分别假设为U和I。然后就另外把电阻箱接入电路中，滑动变阻器不要移动，保持原样，调整变阻器的阻值，使得电压和电流为I和U。

在电路分析中，最基本的电路就是电阻电路。而分析电阻电路常常要将电路化简，求其等效电阻。由于实际电路形式多种多样，电阻之间联接方式也不尽相同，因此等效电阻计算方法也有所不同。本文就几种常见的电阻联接方式，谈谈等效电阻的计算方法和技巧

九、等效电阻法？

几个连接起来的电阻所起的作用，可以用一个电阻来代替，这个电阻就是那些电阻的等效电阻。也就是说任何电回路中的电阻，不论有多少只，都可等效为一个电阻来代替。而不影响原回路两端的电压和回路中电流强度的变化。这个等效电阻，是由多个电阻经过等效串并联公式，计算出等效电阻的大小值。也可以说，将这一等效电阻代替原有的几个电阻后，对于整个电路的电压和电流量不会产生任何的影响，所以这个电阻就叫做回路中的等效电阻。

　　就是用一个电阻代替串联电路中几个电阻，比如一个串联电路中有2个电阻，可以用另一个电阻来代替它们。首先把这两个电阻串联起来，然后移动滑动变阻器，移动到适当的地方就可以，然后记录下这时的电压与电流，分别假设为U和I。然后就另外把电阻箱接入电路中，滑动变阻器不要移动，保持原样，调整变阻器的阻值，使得电压和电流为I和U。

在电路分析中，最基本的电路就是电阻电路。而分析电阻电路常常要将电路化简，求其等效电阻。由于实际电路形式多种多样，电阻之间联接方式也不尽相同，因此等效电阻计算方法也有所不同。

十、二极管等效电阻一般多大？

等效电阻可分为直流等效电阻和交流等效电阻，0.07Ω 是直流等效电阻，交流等效电阻要比直流等效电阻小